Bestimmung von linearen Funktionstermen
Bestimmung des Funktionsterms anhand eines Punktes und der Steigung
Beispiel:
Der Graph einer linearen Funktion \(f\) enthält den Punkt \(P(4| 8)\) und hat die Steigung \(3\).
Bestimmen Sie den Funktionsterm.
Methode 1: Mit der allgemeinen Form
Schrittfolge:
1. Ansatz: \(f(x)=mx+t\)
2. \(m\) einsetzen
3. Koordinaten von \(P(x|y) \) einsetzen
Im Beispiel:
\(f(x)=mx+t\)
\(m = 3\) einsetzten: \(f(x)=3x+t\)
Koordinaten von \(P(4| 8)\) einsetzen:
\(8=3 \cdot 4+t \quad\Rightarrow\quad t = -4\)
\( \quad\Rightarrow\quad f(x)=3x-4\)
Methode 2: Mit der Punkt-Steigungs-Form
Durch den Ansatz mit der Punkt-Steigungs-Form wird das Aufstellen des Funktionsterms besonders einfach.
Die gegebene Steigung und die Koordinaten des Punktes müssen hier einfach nur eingesetzt werden.
Schrittfolge:
1. Ansatz: \(f(x)=m(x-x_0)+y_0\)
2. \(m\) einsetzen
3. Koordinaten von \(P(x_0| y_0) \) einsetzen
Im Beispiel:
\(f(x)=m(x-x_0)+y_0\)
\(m = 3\) einsetzen: \(f(x)=3(x-x_0)+y_0\)
Koordinaten von \(P(4|8)\) einsetzen:
\(f(x)=3(x-4)+8 =3x-4\)
Übung 1
Bestimmung des Funktionsterms anhand von zwei Punkten
Beispiel:
Der Graph einer linearen Funktion \(f\) geht durch die Punkte \(P(-2| 10)\) und \(Q(4| -5)\).
Bestimmen Sie einen möglichen Funktionsterm.
Methode 1: Mit der allgemeinen Form
Schrittfolge:
1. Ansatz: \(f(x)=mx+t\)
2. \(m = \frac \) berechnen und einsetzen
3. z. B. Koordinaten von \(P(x| y) \) einsetzen
Im Beispiel:
\(f(x)=mx+t\)
\(m = \frac = \frac = \frac =-2,5\)
\(f(x)=-2,5x+t\)
Koordinaten von \(P(-2| 10)\) einsetzen:
\(10=-2,5 \cdot (-2) +t \quad\Rightarrow\quad t = 5\)
\( \quad\Rightarrow\quad f(x)=-2,5x+5\)
Methode 2: Mit der Punkt-Steigungs-Form
Schrittfolge:
1. Ansatz: \(f(x)=m(x-x_0)+y_0\)
2. \(m = \frac = \frac \) berechnen und einsetzen
3. z. B. Koordinaten von \(P(x_0| y_0) \) einsetzen
Im Beispiel:
\(f(x)=m(x-x_0)+y_0\)
\(m = \frac = \frac = \frac =-2,5\)
\(f(x)=-2,5(x-x_0)+y_0\)
Koordinaten von \(P(-2| 10)\) einsetzen:
\(f(x)=-2,5 (x-(-2))+10 =-2,5 (x+2)+10\)
\( \quad\Rightarrow\quad f(x)=-2,5x+5\)
Übung 2
Funktionsterm anhand eines vorgegebenen Graphen bestimmen
Beispiel:
Bestimmen Sie die Funktionsgleichung der abgebildeten Geraden.
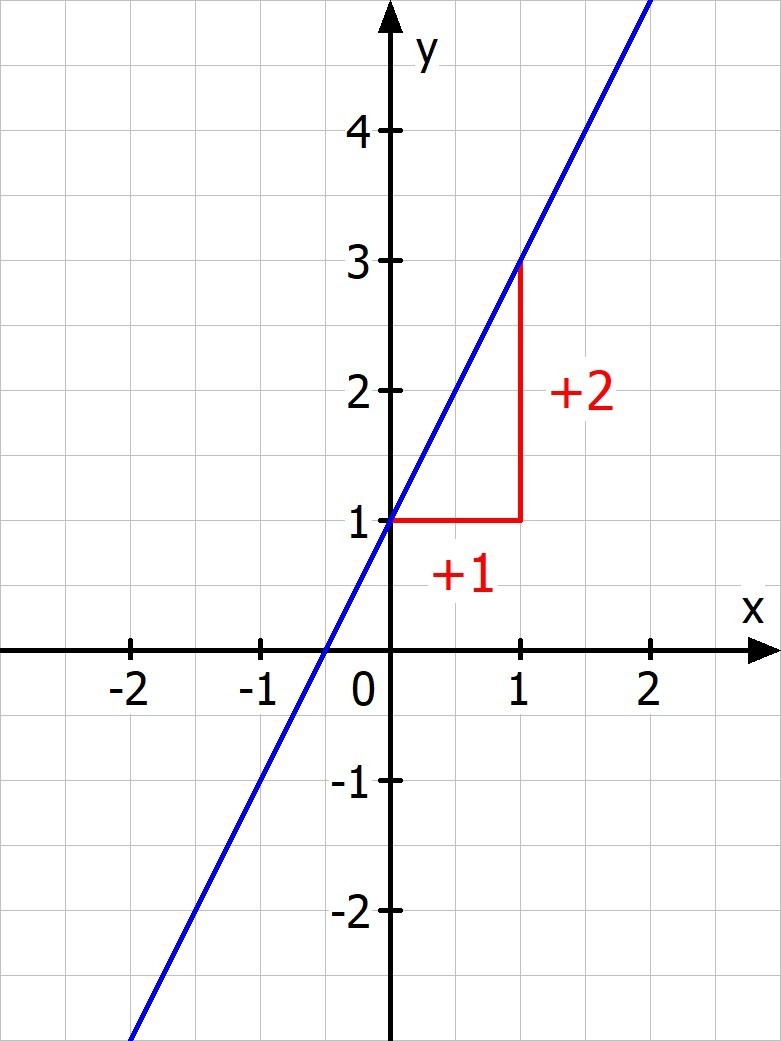
Schrittfolge:
1. Ansatz: \(f(x)=mx+t\)
2. Steigung m:
Ermittlung mit einem Steigungsdreieck.
3. y-Achsenabschnitt t:
Direktes Ablesen am Graphen.
Im Beispiel:
\(f(x)=mx+t\)
\(m=\frac =\frac=2\)
\(t = 1\)
\(\Rightarrow f(x)=2x+1\)
Interaktive Übung
Auftrag:
Ermitteln Sie den passenden Funktionsterm zur dargestellten Gerade.
Hinweise zum Applet:
- Dieses Applet erzeugt zufällig Graphen von linearen Funktionen.
- Der y-Wert eines Punktes P auf der Geraden wird exakt angezeigt. Der Punkt P kann auf der Geraden verschoben werden.
- Für die Berechnung des konstanten Vorfaktors kann optional eine Eingabezeile eingeblendet werden (dazu bitte ein Häkchen bei “Nebenrechnung” setzen).
- Die Lösungsschaltfläche wird nur angezeigt, wenn die Eingabe für Nebenrechnungen ausgeschaltet wird.
Alle Materialien auf der Webseite vibos.de, die auch als solche gekennzeichnet sind, stehen als OER – Open Educational Resources zur freien Verfügung und unter Creative Commons-Lizenz. Sie dürfen unter Angabe der Herkunft [CC BY SA 4.0 VIBOS – Virtuelle Berufsoberschule Bayern] weiterverwendet und verlinkt werden.



